On the Surprising Effectiveness of Large Learning Rates under Standard Width Scaling

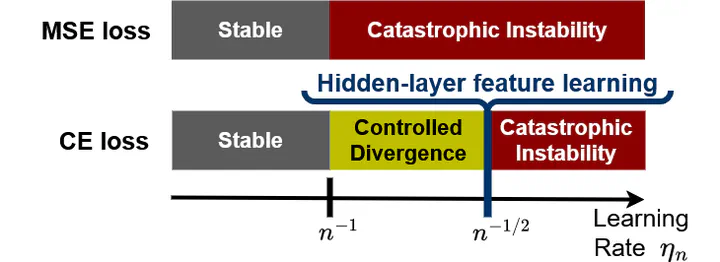
A primary goal of infinite-width theory has always been explaining neural networks as they are initialized and trained in practice (called ‘standard parameterization’, short SP). But there has always remained a fundamental gap: Existing theory for SP predicts a kernel regime with vanishing feature learning under small learning rates, and logit divergence under large learning rates. But even extensively large models continue to effectively learn features in practice, which results in favorable performance at scale. While previous works suggest strong finite-width or long-training time effects, we show that these explanations do not suffice. Instead this apparent gap between infinite-width theory and practice can be fundamentally reconciled by proving that logit divergence does not harm training stability when using torch.nn.CrossEntropyLoss. Consequently even extensively wide neural networks in SP trained with SGD (or Adam) under large learning rates effectively update all hidden layers. This has several important implications:

a) The maximal-stable learning rate constrains the optimal learning rate which significantly reduces the search space for the optimal learning rate, even in practical settings like GPT pretraining. The optimal learning rate often even ‘approximately transfers’ across model scale under the scaling exponents predicted by our theory despite vanishing input layer feature learning and logit blowup in SP with large learning rates (for both SGD and Adam).

b) CE loss often outperforms MSE loss because large learning rates do not remain stable under MSE loss and feature learning is lost at scale. Using muP at large model scale enables using other loss functions such as MSE loss.

c) We explain why SP-full-align from Everett et al. works so well: It remains stable because logit divergence does not harm training stability. It approximately transfers the optimal learning rate because it preserves width-independent updates in the regime width « output dimension.

d) Overall, Tensor Program width-scaling exponent predictions for layerwise updates and even maximal stable learning rates hold surprisingly accurately already at moderate scale and over the course of training. This allows predicting sources of training or numerical instability and finding principled solutions.

These insights uncover many exciting questions for future work. For example, training points are memorized increasingly sharply with model scale. On the one hand this might speed up learning, but on the other hand it hurts calibration. Overall, when does logit divergence help and when does it harm performance? Is this a fundamental reason for overconfident predictions in SP, and muP might be more calibrated? Similarly, should we boost input- and normalization layer learning rates at large scale, or is it a beneficial inductive bias to learn these weights increasingly slowly in large models?